
Neutrinos can also interact outside the detector, in the surrounding rock. If they're muon neutrinos, the resulting muon can penetrate the rock and be seen in Super-K. While muons from interactions above the detector cannot be sorted out from the continuous rain of muons created in cosmic ray showers in the atmosphere above the mountain, muons coming from below can only be due to neutrino interactions, since cosmic ray muons can't make it through from the other side of the earth. Here's an example of a neutrino-induced up-going muon:

Muons are very penetrating particles, and so might be produced by a neutrino interaction quite some distance from the detector. Thus, the effective target volume for observing neutrino interactions using up-going muons is much larger than the detector itself, and grows with the energy of the neutrino (since higher energy neutrinos produce higher energy muons, which can travel through more rock). This results in the up-going muon data probing a far higher range in energy than the contained event analysis.
The penalty paid for this large energy range is that it is not possible to measure the energy of each muon, since it spends only a small part of its time in the detector itself. However, if an up-muon stops in the detector rather than blasting all the way through, it is likely to have come from a lower energy parent neutrino. Thus, the up-muon sample can be divided into two data sets - a high-energy "through-going muon" set, and a medium-energy "stopping muon" set. Note that the contained events are mostly less than 10 GeV, forming a well studied low-energy set. While each individual neutrino cannot have its energy measured by looking at the up-muons, it is possible to calculate the likely energy spectrum of the parent neutrinos:
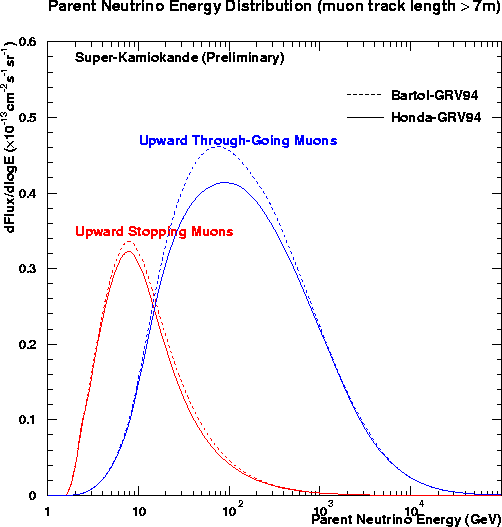
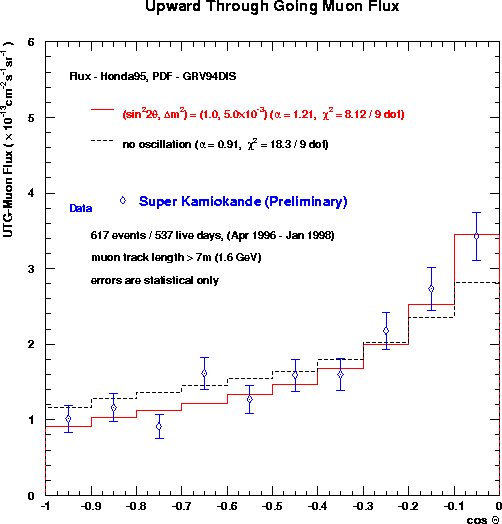
If neutrinos have mass and thus oscillate between flavors, the chance that a muon neutrino has oscillated into something else by the time it gets to near Super-K is larger the further it has traveled, and the lower its energy. Thus, there should be fewer muons coming from straight up than from near the horizon - they've had to travel further, so have had more of a chance to oscillate to something else, such as a tau neutrino, which Super-K cannot detect. In this plot of the arrival direction of Super-K's upmus, compare the shapes of the observed (data points) and expected (black dashed line) distributions, and notice that there are comparatively fewer muons coming straight up - as predicted in the case of neutrino oscillations (red line).
Also, since the stopping muons come from lower energy neutrinos which have a much better chance to oscillate away, there should be too few stopping muons. Calculating the ratio of stopping to through-going upmus gives another test of oscillations. Here's this data. The ratio seen in the data is far less than the expected, but matches the oscillation predictions well.
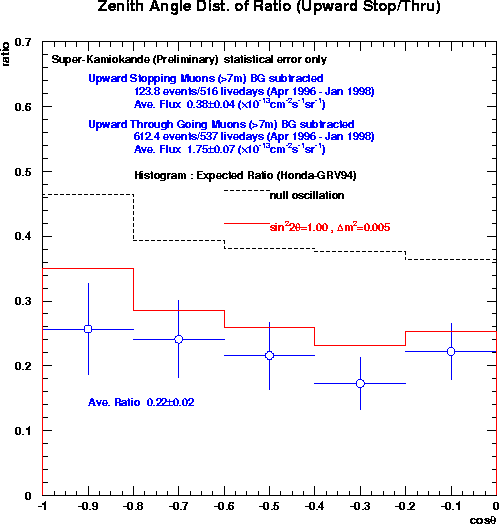
If one estimates what oscillation parameters are needed to explain the observed Super-K upward going muon data, the answer is compatible with that given by the contained event analysis. The no-oscillations case is ruled out at ~98% by the through-going muon shape, and at >99% by the stopping/through-going ratio.
Here's a postscript file of the Super-K up-going muon data presented in a poster at the Neutrino 98 conference in Takayama, Japan, with more details of this analysis.
Comments to habig@budoe.bu.edu .