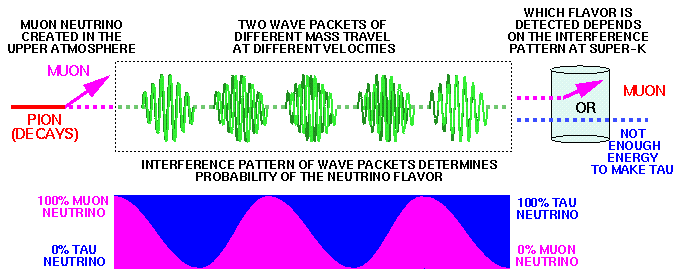

The way neutrinos interact depends on a property called their "flavor". Electron "flavored" neutrinos participate in interactions that involve electrons, muon "flavored" neutrinos participate in interactions that involve muons, and similarly for tau neutrinos. The pion always decays to a muon and a muon-neutrino (well, almost always, 99.99% of the time). The muon neutrino interacts with a nucleus to make a muon, not an electron. This is also called conservation of lepton number. But it seems the neutrino is composed of a combination of two or three different mass states. The way a neutrino propagates from one place to another depends on the mass states. But quantum mechanics tells us that if two (or more) neutrinos are composed of the same mass states but in different combinations, then the neutrino can oscillate from one flavor to another while it travels through space.
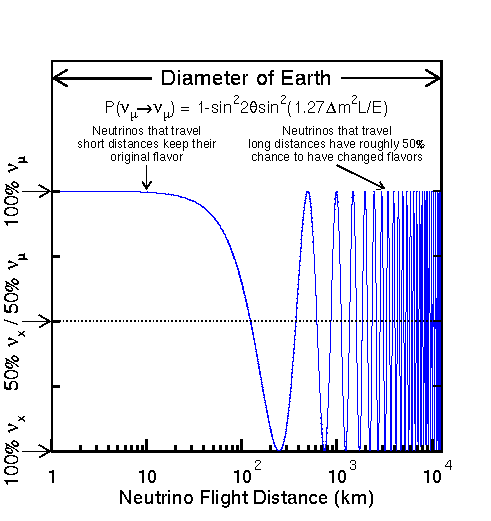
Which flavor will it be when it interacts in the detector? The answer must be calculated quantum mechanically, and therefore it involves a probability. The probability formula for two-flavor oscillation is given below. It depends on sin^2 2*theta, which governs the strength of the mixing if the two states. And it depends on delta-m^2 which is the difference in mass^2 between the two states. Finally, it depends on the ratio of the neutrino energy, E, to the neutrino travel distance, L. High energy neutrinos that travel a short distance (small L/E) are unlikely to change flavors compared to low energy neutrinos that travel a long distance (large L/E).